Qualitative analysis is the process through which the quality of a substance is determined, e.g., detecting the presence of carbon, hydrogen, oxygen…

Quantitative analysis is the process through which we determine the percentage composition of the elements in a substance or the concentration of a solution, e.g., hematological analyses, measurements of sugars/proteins in food, etc.

Titration: It is a method of quantitative analysis. Using this method, the unknown concentration of a substance is determined by adding a solution of known concentration with which it reacts stoichiometrically.

Εxperimental procedure

Glassware:

• Beaker
• Funnel
• Conical Flask
• Burette
• Volumetric Cylinder
• Magnetic Stirrer

For more information about the glassware, check out our laboratory guide

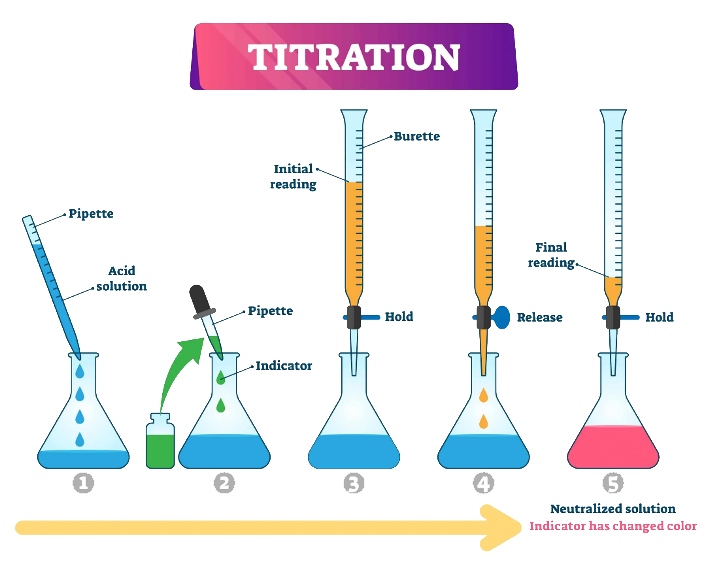
Terminologies

• If you wish to find the concentration of an acid solution, you will titrate the acid solution with a solution of a base (alkali) of known concentration—alkalimetry.
• You titrate a base of unknown concentration with an acid of known concentration—acidimetry
• Titrant: a solution of a known concentration, which is added to another solution whose concentration must be determined.
• Titrand or analyte: the solution whose concentration must be determined.
• Equivalence point: point in titration at which the amount of titrant added is just enough to completely neutralize the analyte solution. At the equivalence point in an acid-base titration, moles of base = moles of acid, and the solution only contains salt and water.

Possible Errors in Titration

For monoprotic acids and bases, it is true that

\(C_a \cdot V_a = C_k \cdot V_k => C_a = \frac{C_k \cdot V_k}{V_a}\)

Where a is the unkown solution and k is the known solution.

\(C_k\) and \(V_k\) are constants, and so the errors are caused by \(V_a\)

If \(C_a\) in the experiment is

• greater than the actual value => positive error
• lower than the actual value => negative error

Types of titrations

Titration of a strong acid with a strong base

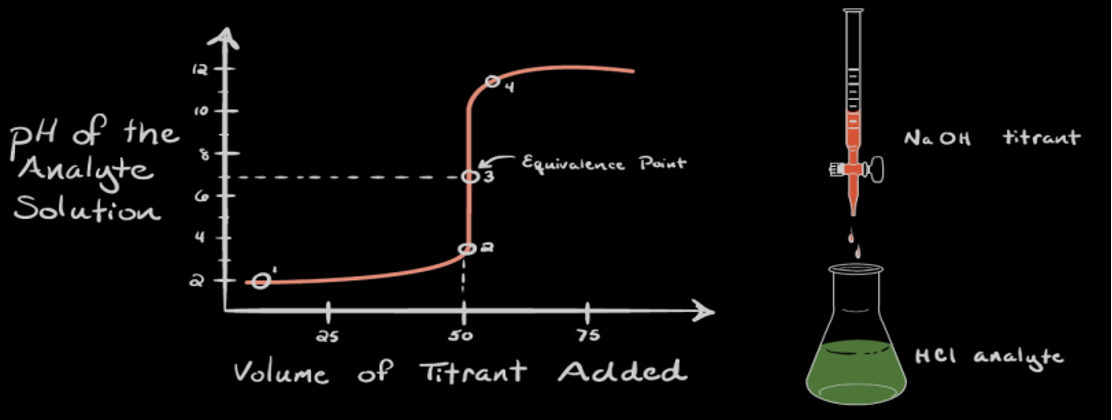
Point 1: No NaOH added yet, so the pH of the analyte is low (it predominantly contains H3O+ from dissociation of HCl).

Point 2: This is the pH recorded at a time point just before complete neutralization takes place.

Point 3: This is the equivalence point (halfway up the steep curve). At this point, moles of NaOH added = moles of HCl in the analyte. At this point, \(\ce{H3O^+}\) is completely neutralized by \(OH^-\). The solution only has salt (NaCl) and water, and therefore the pH is neutral, i.e., pH = 7.

Point 4: Addition of NaOH continues, and pH starts becoming basic because HCl has been completely neutralized and now an excess of OH⁻ is present in the solution (from dissociation of NaOH).

Weak Acid with Strong Base

There are four parts to the titration curve of a weak acid (analyte) with a strong base (titrant).

1. Initial pH (pH of a weak acid)
2. Buffer Equation (Henderson-Hasselbalch Eq.)
3. Equivalence Point (salt of weak acid)
4. Excess Base (pH based on concentration of excess titrant)

Pure Acid

Treat as a weak acid.

\[pH= -log \sqrt{(K_a \cdot C_a)}\]

Buffer Region

One way to make a buffer is to partially neutralize an acid, and so in the buffer region we can use the Henderson-Hasselbalch equation.

\[pH = pK_a + log \frac{[base]}{[acid]}\]

Half equivalence

In a titration this is known as half equivalence or half titer, which is the volume required to titrate off half of the titratable protons (of a monoprotic acid or the first proton of a polyprotic acid). That is, at half equivalence, \(V_b = \frac{V_{eq}}{2}\)

\(pH_{at half titer} = pK_a + log \frac{V_b}{V_{eq} - V_b}\)

\(= pK_a + log \frac{\frac{V_{eq}}{2}}{V_{eq} - \frac{V_{eq}}{2}}\)

\(= pK_a + log \frac{\frac{V_{eq}}{2}}{\frac{V_{eq}}{2}}\)

\(= pK_a + log 1\)

\(= pK_a\)

The method used for weak base + strong acid is very similar to that presented before.

Weak acid + weak base titrations involve some more complicated (but not too complicated) acid-base equilibria calculations.

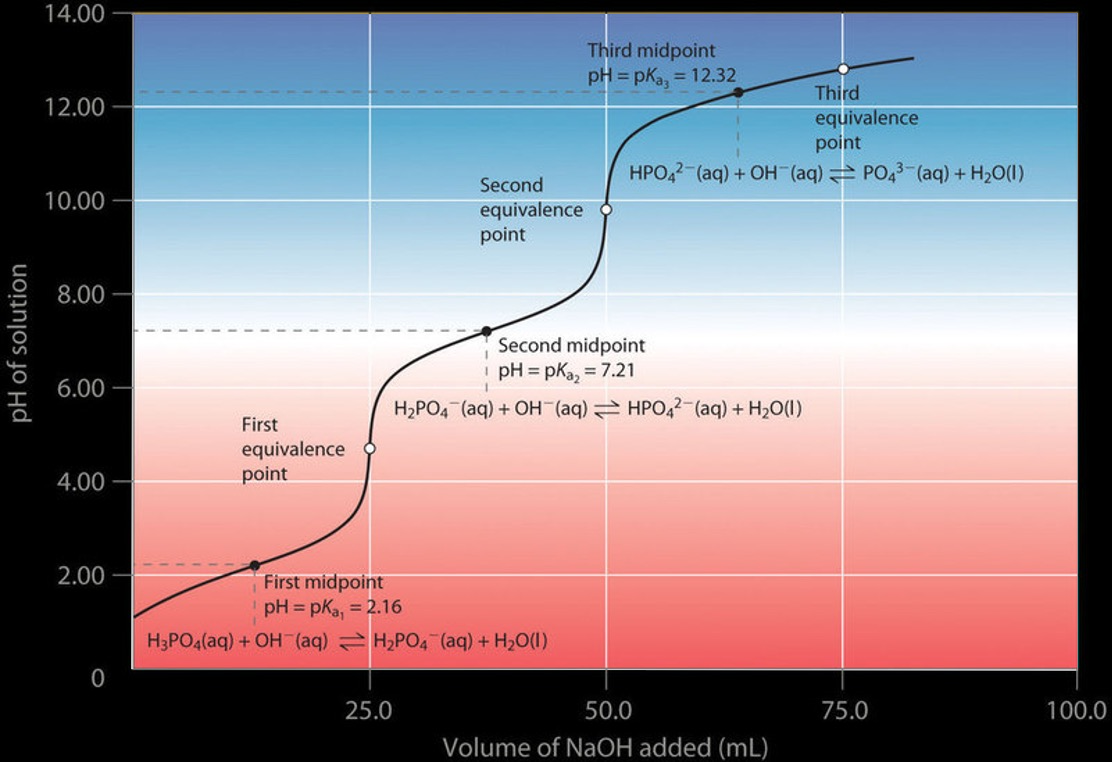
Polyprotic Titration Curves

Each proton had its own ionization constant, with

\(K_{a_1} > K_{a_2} > K_{a_3}\)

This results in a titration curve like that of the figure. If each subsequent \(K_a\) is at least 1000 times smaller than the previous, then the protons are taking off stepwise, and there would be a unique equivalence point for each step. In a monoprotic titration, the base after the equivalence point is in excess, and the solution quickly becomes basic. But if there is a leveling off, that could indicate another titratable proton.

Written by Fillios Memtsoudis